Option A:
 is the expression that correctly uses the formula
is the expression that correctly uses the formula
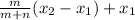
Step-by-step explanation:
It is given that, the number line segment from Q to S has endpoints Q at –14 and S at 2.
Point R partitions the directed line segment from Q to S in a 3:5 ratio.
Thus, we have,
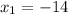 ,
,
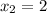 ,
,
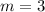 and
and

The location of point R can be determined using the formula,
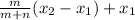
Substituting the values, we get,

Hence, substituting the values
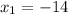 ,
,
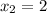 ,
,
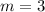 and
and
 in the formula
in the formula
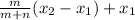 , we get,
, we get,

Thus, the expression that correctly uses the formula is

Therefore, Option A is the correct answer.