Answer:
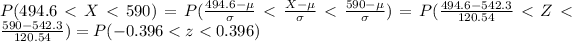
And we can find this probability with this difference:
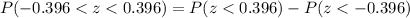
And in order to find these probabilities we can use tables for the normal standard distribution, excel or a calculator.

Explanation:
Assuming that we have the following info: "The admissiones committees for most masters of business administration (MBA) programs requires the Graduate Management Admission Test (GMAT) as part of the application for new students. It has been shown that the scores on GMAT ar enormally distributed with a mean of 542.3 and a standard deviation of 120.54"
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Solution to the problem
Let X the random variable that represent the scores for GAMT of a population, and for this case we know the distribution for X is given by:
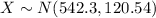
Where
 and
and
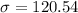
We are interested on this probability
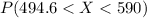
And the best way to solve this problem is using the normal standard distribution and the z score given by:

If we apply this formula to our probability we got this:
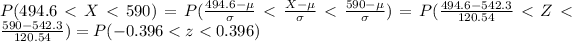
And we can find this probability with this difference:
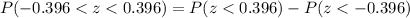
And in order to find these probabilities we can use tables for the normal standard distribution, excel or a calculator.
