Answer:
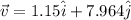
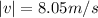
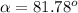 north of east
north of east
Step-by-step explanation:
Let i and j be the unit components of east and north directions, respectively. We can calculate the velocity components of ocean current:
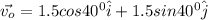
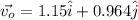
The velocity vector for ship with respect to water is
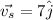
So the velocity vector of the ship with respect to Earth is the sum vector of velocity of ship with respect to water and velocity of water with respect to Earth
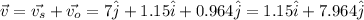
This vector would have a magnitude and direction of:
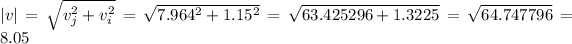
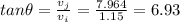
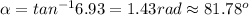 north of east
north of east