Question

If a couple were planning to have three​ children, the sample space summarizing the gender outcomes would​ be: bbb,​ bbg, bgb,​ bgg, gbb,​ gbg, ggb, ggg. a. Construct a similar sample space for the possible gender outcomes​ (using b for boy and g for girl​) of two children. b. Assuming that the outcomes listed in part​ (a) were equally​ likely, find the probability of getting two girl children. c. Find the probability of getting exactly one boy child and one girl child.

Answer 1

(a) The sample space is: S = {bb, bg, gb, gg}

(b) The probability that the couple has two girl children is 0.25.

(c) The probability that the couple has exactly 1 boy and 1 girl child is 0.50.

Explanation:

A boy child is denoted by, b.

A girl child is denoted by, g.

(a)

A couple has two children.

The sample space for the possible gender of the two children are:

The couple can have two boys, two girls or 1 boy and 1 girl.

So the sample space is:

S = {bb, bg, gb, gg}

(b)

It is provided that the outcomes of the sample space S are equally likely, i.e. each outcome has the same probability of success.

Compute the probability that the couple has two girl children as follows:

P (2 Girls) = Favorable no. of outcomes ÷ Total no. of outcomes

`=(1)/(4) \\=0.25`

Thus, the probability that the couple has two girl children is 0.25.

(c)

Compute the probability that the couple has exactly 1 boy and 1 girl child as follows:

P (1 boy & 1 girl) = Favorable no. of outcomes ÷ Total no. of outcomes

`=(2)/(4) \\=0.50`

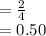
Thus, the probability that the couple has exactly 1 boy and 1 girl child is 0.50.