Question

The amount of time it takes for an investment to double in value is called the doubling time for the investment. If the doubling time for a $10,000 investment is seven years and the interest on the investment is compounded annually, what must be the annual rate of interest?

Answer 1

Compounding interest rate, r = 10.41%

Step-by-step explanation:

As the investment will be doubled after 7 years from now, the future value of the current investment will be = $10,000 × 2 = $20,000

Therefore,

Number of periods (years), n = 7

Future value, FV = $20,000

Principal = Present Value, PV = $10,000

we have to determine the compounding interest rate, r.

We know,

r =
`[((FV)/(PV))^{(1)/(n)} - 1]`

Putting the values into the formula, we can get,

r =
`[((20,000)/(10,000))^{(1)/(7)} - 1]`

or, r =
`(2^{(1)/(7)} - 1)`

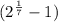
With the help of calculator, we can find the value of
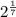`2^{(1)/(7)}` = 1.1041

or, r = (1.1041 - 1)

or, r = 0.1041

Therefore, interest rate = 10.41%