Question

A cylindrical specimen of this alloy 12.7 mm in diameter and 250 mm long is stressed in tension and found to elongate 7.6 mm. On the basis of the information given, is it possible to compute the magnitude of the load that is necessary to produce this change in length? If so, calculate the load. If not, explain why.

Answer 1

Condition 2 is true.

`\epsilon_(test)>\epsilon_(yield)`

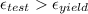
we can not calculate the load with given information.

According to above values, Condition 2 is satisfied so we can not find the load with given information because material deformation lies in plastic region.

Step-by-step explanation:

In order to check whether we can find the load or not we have to check the following conditions:

Condition 1:

`\epsilon_(test)<\epsilon_(yield)`

If this condition is true then we can calculate the load.

Condition 2:

`\epsilon_(test)>\epsilon_(yield)`

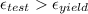
If this condition is true then we can not calculate the load with given information.

Calculating
`\epsilon_(test)`:

`\epsilon_(test)=(Elongation)/(original\ length)`

`\epsilon_(test)=(7.6\ mm)/(250\ mm)\\ \epsilon_(test)=0.0304`

Calculating
`\epsilon_(yield)`:

`\epsilon_(yield)=(Yield\ Stress)/(Elastic\ modulus)\\ \epsilon_(yield)=(280\ Mpa)/(105*10^3\ MPa) \\\epsilon_(yield)=2.67*10^(-3)=0.00267`

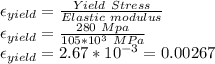
Hence:

Condition 2 is true.

`\epsilon_(test)>\epsilon_(yield)`

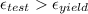
According to above values, Condition 2 is satisfied so we can not find the load with given information because material deformation lies in plastic region.