Question

engine emits sound uniformly in all directions, radiating an acoustic power of 3.65 × 10 5 W. 3.65×105 W. Find the intensity of the sound at a distance of 52.7 m 52.7 m from

Answer 1

10.46W/m²

Step-by-step explanation:

The intensity (I) of a sound is related to the power (P) radiated by the sound within an area (A) as follows;

I =
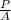`(P)/(A)` ----------------(i)

But;

A = 4
`\pi` r²

Where;

r is the specified distance covered by the sound.

Substitute A = 4
`\pi` r² into equation (i) to get;

I =
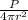`(P)/(4\pi r^(2) )` ------------------------(ii)

From the question;

P = acoustic power = 3.65 x 10⁵W

r = 52.7m

To calculate the intensity of the sound, take
`\pi` = 3.142 and substitute other values into equation (ii) as follows;

I =
`(3.65*10^5)/(4*3.142*52.7^2)`

I =
`(3.65*10^5)/(34904.98)`

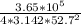
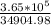
I = 10.46W/m²

Therefore, the intensity of the sound at that distance is 10.46W/m²

Answer 2

130.2dB

Step-by-step explanation:

The formula for determining the intensity of a wave is expressed as

`I=(P)/(A)\\`

Where P is the power in watts, and A is the area of the sphere formed by the wave

Data given

Power,P=3.65*10^5W

distance,d=52.7

Hence since the distance represent the radius, we can determine the area of the sphere formed

`A=4\pi r^(2)\\A=4\pi *52.7^(2)\\A=34900.45m^2`

The intensity can be computed as

`I=(3.65*10^5)/(34900.45)\\ I=10.46W/m^2`

we can convert to decibel

`I=10log(10.46)/(10^(-12)) \\I=130.2dB`