Question

Set up the integral that uses the method of cylindrical shells to find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line.

x = (y − 5)2, x = 4; about y = 3


Use the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about the specified axis.


y = x2, x = y2; about y = −7

Answer 1

first exercise

V = 16 π

second exercise

V= 68π/15

Explanation:

Initially, we have to plot the graph x = (y − 5)2 rotating around y = 3 and the limitation x = 4

vide picture 1

The rotation of x = (y − 5)2 intersecting the plane xy results in two graphs, which are represented by the graphs red and blue. The blue is function x = (y − 5)2. The red is the rotated cross section around y=3 of the previous graph. Naturally, the distance of "y" values of the rotated equation is the diameter of the rotation around y=3 and, by consequence, this new red equation is defined by x = (y − 1)2.

Now, we have two equations.

x = (y − 5)2

xm = (y − 1)2 (Rotated graph in red on the figure)

The volume limited by the two functions in the 1 → 5 interval on y axis represents a volume which has to be excluded from the volume of the 5 → 7 on y axis interval integration.

Having said that, we have two volumes to calculate, the volume to be excluded (Ve) and the volume of the interval 5 → 7 called as V. The difference of V - Ve is equal to the total volume Vt.

(1) Vt = V - Ve

Before start the calculation, we have to take in consideration that the volume of a cylindrical shell is defined by:

`(2) V=\int\limits^{y_(1) }_{y_(2)}{2*pi*y*f(y)} \, dy`

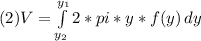
f(y) represents the radius of the infinitesimal cylinder.

Replacing (2) in (1), we have

`V= \int\limits^(5 )_{{3}}{2*pi*y*(y-5)^(2) } \, dy - \int\limits^(7 )_{{5}}{2*pi*y*(y-5)^(2) } \, dy`

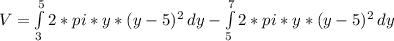
V = 16 π

----

Second part

Initially, we have to plot the graph y = x2 and x = y2, the area intersected by both is rotated around y = −7. On the second image you can find the representation.

vide picture 2

As the previous exercise, the exclusion zone volume and the volume to be considered will be defined by the interval from x=0 and y=0, to the intersection of this two equations, when x=1 and y = 1.

The interval integration of equation y = x2 will define the exclusion zone. By the other hand, the same interval on the equation x=y2 will be considered.

Before start the calculation, we have to take in consideration that the volume of a cylindrical shell is defined by:

`(3) V=\int\limits^{x_(1) }_{x_(2)}{2*pi*x*f(x)} \, dx`

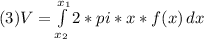
Notice that in the equation above, x and y are switched to facilitate the calculation. f(x) is the radius of the infinitesimal cylinder

Having this in mind, the infinitesimal radius of equation (3) is defined by f(x) + radius of the revolution, which is 7. The volume seeked is the volume defined by the y = x2 minus the volume defined by x=y2. As follows:

`V= \int\limits^(1 )_{{0}}{2*pi*x*(√(x) + 7) } \, dy - \int\limits^(1 )_{{0}}{2*pi*x*(x^(2)+7) } \, dy`

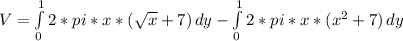
V= 68π/15