Question

The number of customers at your company's store on a given day has a bell-shaped normal distribution with a mean of 60 and a standard deviation of 10. What percentage of days do you expect to have between 50 and 70 customers? Give your answer as a percent, but do not incude the % sign.

Answer 1

Percentage of days we can expect to have between 50 and 70 customers = 68.3 .

Explanation:

We are given that the number of customers at your company's store on a given day has a bell-shaped normal distribution with a mean of 60 and a standard deviation of 10 i.e.;

Mean,
`\mu` = 60 and Standard deviation,
`\sigma` = 10

Since, distribution is normal so;

Z score =
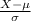`(X -\mu)/(\sigma)` ~ N(0,1)

Let X = Number of customers

So, Probability(between 50 and 70) = P(50 <= X <= 70) = P(X<=70) - P(X<=50)

P(X <= 70) = P(
`(X -\mu)/(\sigma)` <=
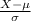`(70 -60)/(10)` ) = P(Z <= 1) = 0.84134

P(X <= 50) = P(
`(X -\mu)/(\sigma)` <=
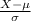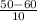`(50 -60)/(10)` ) = P(Z <= -1) = 1 - P(Z <= 1) = 1 - 0.84134 = 0.15866

So, Probability(between 50 and 70) = 0.84134 - 0.15866 = 0.68268 or 68.3%

Therefore, 68.3 percentage of days have customers between 50 and 70.

Answer 2

68

Explanation:

The Empirical Rule states that, for a normally distributed random variable:

68% of the measures are within 1 standard deviation of the mean.

95% of the measures are within 2 standard deviation of the mean.

99.7% of the measures are within 3 standard deviations of the mean.

In this problem, we have that:

Mean = 60

Standard deviation = 10

What percentage of days do you expect to have between 50 and 70 customers?

50 = 60 - 10

So 50 is one standard deviations below the mean.

70 = 60 + 10

So 70 is one standard deviation above the mean.

By the Empirical Rule, 68% of days do you expect to have between 50 and 70 customers. So the answer is 68