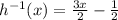Question

Can anyone answer me this question ​

Answer 1

Question 1:

For this case we have the following functions:

`f (x) = 4x + 1\\g (x) = x ^ 3 + 1`

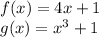
We must find
`g_ {o} f (0`):

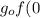By definition we have to:

`g_ {o} f = g (f (x))\\f_ {o} g = f (g (x))`

`g (f (x)) = (4x + 1) ^ 3 + 1`

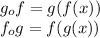
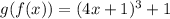
We substitute
`x = 0`:

`g (f (0)) = (4 (0) +1) ^ 3 + 1 = 1 ^ 3 + 1 = 2`

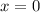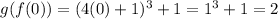
So, we have that
`g (f (0)) = 2`

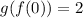
Answer:

`g (f (0)) = 2`

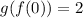
Question 2:

For this case we have the following functions:

`f (x) = 4x + 1\\g (x) = x ^ 3 + 1`

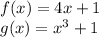
We must find
`f_ {o} g (0)`:

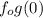By definition we have to:

`f_ {o} g = f (g (x))\\f (g (x)) = 4 (x ^ 3 + 1) + 1 = 4x ^ 3 + 4 + 1 = 4x ^ 3 + 5`

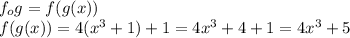
We substitute
`x = 0`:

`f (g (0)) = 4 (0) ^ 3 + 5 = 5`

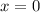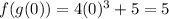
Answer:

`f (g (0)) = 5`

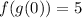
Question 3:

For this case we must find the inverse of the following function:

`h (x) = \frac {2x + 1} {3}`

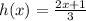
To do this, we follow the steps below:

We change y for
`h (x)`:

`y = \frac {2x + 1} {3}`

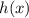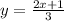
We exchange variables:

`x = \frac {2y + 1} {3}`

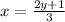
We clear the value of the variable "y":

`3x = 2y + 1\\3x-1 = 2y\\y = \frac {3x} {2} - \frac {1} {2}`

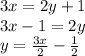
We change y for
`h^( -1) (x)`:

`h ^( - 1) (x) = \frac {3x} {2} - \frac {1} {2}`

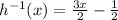
Answer:

`h ^ {- 1} (x) = \frac {3x} {2} - \frac {1} {2}`