Question

A force of F = 125 N is used to drag a crate 3.0 m across a floor. The force is directed at an angle upward from the crate so the vertical part of the force is Fv = 65 N and the horizontal part of the force is Fh = 107 N. How much work is done on the box?

Answer 1

321Nm

Step-by-step explanation:

The work done (W) on an object is the product of the force (F) acting on it and the distance (s), in the direction of the force, covered by the object. i.e

W = F x s -----------------(i)

But from the question:

(i) the object is the box (crate),

(ii) the direction of motion of the box is horizontal,

(iii) the force acting is directed at an angle and it has a vertical component(
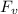`F_(v)`) = 65N and horizontal component (
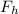`F_(h)`) = 107N.

Now;

Since the box is moving horizontally, the horizontal component (
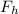`F_(h)`) of the force is the force doing the actual work. In other words, the work is done by the horizontal component of the force.

Therefore, equation (i) can be re-written as;

W =
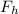`F_(h)` x s -----------------------(ii)

Where;

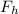`F_(h)` = 107N

s = 3.0m

To calculate the work done, substitute these values into equation (ii) as follows;

W = 107 x 3

W = 321 Nm

Therefore, the amount of work done on the box is 321Nm

Answer 2

Step-by-step explanation:

The forward force to drag is 125N

Distance of 3m.

The distance is on the positive horizontal 3i+0j

The force is directed upward so that the horizontal and vertical component is

Fx=107N and Fy=65N

F=107i+65j

Work done is dot product of Force and distance

Then,

W=F.ds

W=(107i+65j).(3i+0j)

Note i.i=j.j=1, i.j=j.i=0

Therefore

W=107×3+65×0

W=321J

The workdone done on the box is 321J