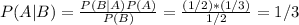Answer:
1/3
Explanation:
Let A be the event that you grab the fair coin and B be the event that you toss a tail.
P(A) is the probability that you grab the fair coin, which is 1/3
P(B) is the probability that you toss a tail, which is 1/2
P(B|A) is the probability that you toss a tail, given that you grab a fair coin, which is 1/2
P(A|B) is the probability that you grab the fair coin, given that you toss a tail, which we are looking for.
Using Bayes probability theorem we have: