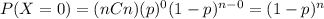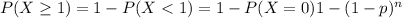Question

The probability that a grader will make a marking error on any particular question of a multiple-choice exam is 0.15. If there are ten questions and questions are marked independently, what is the probability that no errors are made?r what is the probability that at least one error made? these two probabilities. If there are questions and the probability of a marking error is p rather than 0.15, qive expressions no errors least one error

Answer 1

`P(X=0)=(10C10)(0.15)^(0) (1-0.15)^(10-0)=0.1969`

`P(X \geq 1)= 1-P(X<1) = 1-P(X=0) 1-0.1969=0.8031`

`P(X=0)=(nCn)(p)^(0) (1-p)^(n-0)=(1-p)^n`

`P(X \geq 1)= 1-P(X<1) = 1-P(X=0) 1-(1-p)^n`

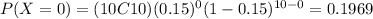
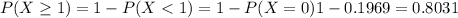
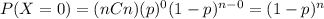
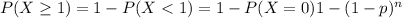
Explanation:

Previous concepts

A Bernoulli trial is "a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted". And this experiment is a particular case of the binomial experiment.

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

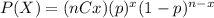
Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

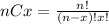
The complement rule is a theorem that provides a connection between the probability of an event and the probability of the complement of the event. Lat A the event of interest and A' the complement. The rule is defined by:
`P(A)+P(A') =1`

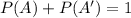
Solution to the problem

Let X the random variable of interest, on this case we now that:

`X \sim Binom(n=10, p=0.15)`

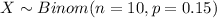
what is the probability that no errors are made?

For this case means that all the questions were correct so we want this probability:

`P(X=0)=(10C10)(0.15)^(0) (1-0.15)^(10-0)=0.1969`

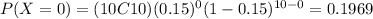
what is the probability that at least one error made?

For this case we want this probability:

`P(X \geq 1)`

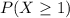
And we can use the complement rule:

`P(X \geq 1)= 1-P(X<1) = 1-P(X=0) 1-0.1969=0.8031`

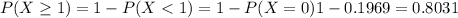
If there are n questions and the probability of a marking error is p rather than 0.15, give expressions for the probabilities of no errors and at least one error

`P(X=0)=(nCn)(p)^(0) (1-p)^(n-0)=(1-p)^n`

`P(X \geq 1)= 1-P(X<1) = 1-P(X=0) 1-(1-p)^n`