Question

The federal government would like to estimate the proportion of households in the U.S. population that own their own homes. A pilot sample of 40 households found that 24 of them owned their homes. Determine the number of households that need to be sampled to construct a 99% interval with a margin of error equal to 3% to estimate the proportion.

Answer 1

1770

Explanation:

We need to estimate number of households to be sampled to construct a 99% confidence interval.

Number of households to be sampled=n=?

`n=\frac{(z_{(\alpha)/(2) })^2 pq }{E^(2) }`

`z_{(\alpha)/(2) } =z_{(\0.01)/(2) }=z_(0.005 )=2.576`

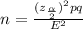
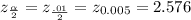
The proportion can be estimated as

p=x/n.

We know that 24 out of 40 households owns their home.

so, x=24 and n=40.

p=24/40

p=0.6

q=1-p=1-0.6=0.4

pq=0.6*0.4=0.24

E=0.03

`n=\frac{(z_{(\alpha)/(2) })^2 pq }{E^(2) }`

`n=(2.576^2(0.24))/(0.03^2)`

`n=(1.5926)/(0.0009)`

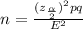
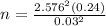
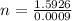
n=1769.56.

n=1770.

Thus, the number of households that need to be sampled are 1770.