Question

Two capacitors with capacitances of 1.0 m F and 0.50 m F, respectively, are connected in series. The system is connected to a 100-V battery. What electrical potential energy is stored in the 1.0- m F capacitor?

Answer 1

The electrical potential energy stored in the 1.0 m F capacitor is 5000 J.

Step-by-step explanation:

When capacitors are connected in series, the total capacitance is given by:

Ctotal = 1 / (1/C1 + 1/C2)

Plugging in the values, we have:

Ctotal = 1 / (1/1.0 mF + 1/0.50 mF)

= 0.67 mF

The voltage across the capacitors in series is the same as the voltage of the battery, which is 100 V. The electrical potential energy stored in a capacitor is given by:

`U = (1/2) * C * V^2`

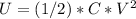
Plugging in the values, we have:

`U = (1/2) * (1.0 mF) * (100 V)^2`

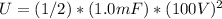
= 5000 J

Therefore, the electrical potential energy stored in the 1.0 mF capacitor is 5000 J.

Answer 2

Therefore energy is stored in the 1.0 mF capacitor is 5.56×10⁻⁹ J

Step-by-step explanation:

Series capacitor: The ending point of a capacitor is the starting point of other capacitor.

If C₁ and C₂ are connected in series then the equivalent capacitance is C.

where
`(1)/(C) =(1)/(C_1)+(1)/(C_2)`

Given that,

C₁ = 1.0 mF=1.0×10⁻³F and C₂ = 0.50mF=0.50×10⁻³F

If C is equivalent capacitance.

Then
`(1)/(C) =(1)/(1.0)+(1)/(0.5)`

`\Rightarrow (1)/(C) =(3)/(1)`

`\Rightarrow C=(1)/(3)` mF

Again given that the system is connected to a 100-v battery.

We know that

q=Cv

q= charge

C= capacitor

v= potential difference

Therefore

`q=((1)/(3) * 10^(-3)*10) C`

`=(10^(-2))/(3) C`

The electrical potential energy stored in a capacitor can be expressed

`U=(q^2C)/(2)`

q= charge

c=capacitance of a capacitor

Therefore energy is stored in the 1.0 mF capacitor is

`U=(q^2C_1)/(2)`

`\Rightarrow U=(((10^(-2))/(3))^2* 10^(-3) )/(2)`

`\Rightarrow U= 5.56* 10^(-9)` J