Answer:
Standard deviation of the sample = 17.421
Explanation:
We are given that in a random sample of 80 teenagers, the average number of texts handled in one day is 50.
Also, the 96% confidence interval for the mean number of texts handled by teens daily is given as 46 to 54.
So, sample mean,
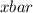 = 50 and Sample size, n = 80
= 50 and Sample size, n = 80
Let sample standard deviation be s.
96% confidence interval for the mean number of texts,
 is given by ;
is given by ;
96% confidence interval for
 =
=
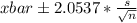
[46 , 54] =
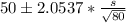
Since lower bound of confidence interval = 46
So, 46 =
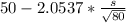
50 - 46 =

s =
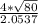 = 17.421
= 17.421
Therefore, standard deviation of the sample is 17.421 .