Question

What is the probability that a simple random sample of 60 unemployed individuals will provide a sample mean within 1 week of the population mean? (Round your answer to four decimal places.)

Answer 1

The question is not complete so I will answer it with an example and a few assumptions. Follow the steps to find the answer to your question.

Important to note:

Your question is a z-scores problem

Assume that for the population of unemployed individuals the population standard deviation is 4 weeks.

Thus, we need to find the z-value.

The z-value is the sample mean decreased by the population mean, divided by the standard deviation that we assumed. So, we have:

`z = (\bar x - \mu)/(\sigma / √(n) ) = (\pm 1)/(4/√(60) ) \approx \pm 1.94`

`P = P(-1 < \bar x - \mu < 1) = P(-1.94 < z < 1.94) = 1 - 2P(z < -1.94)`

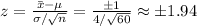
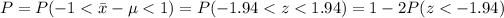
Using any standard negative z-scores table, we can find that:
`P(z < -1.94) = 0.0262`

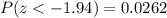
Thus, we get:

`P(| \bar x - \mu | < 1) = 1 - 2 * 0.0262 = 1 - 0.0524 = 0.9476`

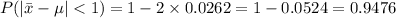
Therefore, the probability that a simple random sample of 60 unemployed individuals will provide a sample mean within 1 week of the population mean is 0.9476

Answer:

0.9476