Solution:
The possibilities are either girl or boy
p(b) = probability of boy =

p(g) = probability of girl=

A) all boys
If all are boys means the 3 children will be boys
Then
P(all boys) =
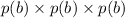
P(all boys) =
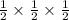
P(all boys) =

B) All boys or all girls
If all are boys means the 3 children will be boys or girls
From eq (1)
P(all boys) =

Similarly ,
P(all girls) =

C) Exactly two boys or two girls
P(Exactly two boys) out of 3 children there will be 2 boys and 1 girl
P(Exactly two boys) =
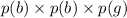
P( Exactly two boys) =
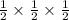
P( Exactly two boys) =

Similarly P(Exactly two Girls ) means out of 3 children there will be 2 girls and 1 boy
P( Exactly two girls) =

D) At least one child of each gender
P(At least one child of each gender) =
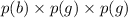
This means among the 3 children there should be one children of different gender. So lets assume out of three children one child be boy and the remaining 2 be girls
Thus
P(At least one child of each gender) =
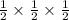 =
=
