Question

A steady, incompressible, two-dimensional velocity field is given by the following components in the x-y plane: u=1.85+2.05x+0.656y v=0.754−2.18x−2.05y . Calculate the acceleration field (find expressions for acceleration components ax and ay), and calculate the acceleration at the point (x,y) = (-1, 5).

Answer 1

1)
`a_x=4.287+2.772x\\a_y=-5.579+2.772y`

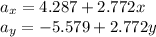
2) 8.418

Step-by-step explanation:

1)

The two components of the velocity field in x and y for the field in this problem are:

`u=1.85+2.05x+0.656y`

`v=0.754-2.18x-2.05y`

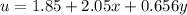
The x-component and y-component of the acceleration field can be found using the following equations:

`a_x=(du)/(dt)+u(du)/(dx)+v(du)/(dy)`

`a_y=(dv)/(dt)+u(dv)/(dx)+v(dv)/(dy)`

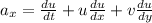
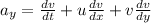
The derivatives in this problem are:

`(du)/(dt)=0`

`(dv)/(dt)=0`

`(du)/(dx)=2.05`

`(du)/(dy)=0.656`

`(dv)/(dx)=-2.18`

`(dv)/(dy)=-2.05`

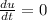
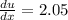
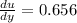
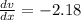
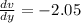
Substituting, we find:

`a_x=0+(1.85+2.05x+0.656y)(2.05)+(0.754-2.18x-2.05y)(0.656)=\\a_x=4.287+2.772x`

And

`a_y=0+(1.85+2.05x+0.656y)(-2.18)+(0.754-2.18x-2.05y)(-2.05)=\\a_y=-5.579+2.772y`

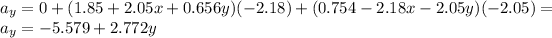
2)

In this part of the problem, we want to find the acceleration at the point

(x,y) = (-1,5)

So we have

x = -1

y = 5

First of all, we substitute these values of x and y into the expression for the components of the acceleration field:

`a_x=4.287+2.772x\\a_y=-5.579+2.772y`

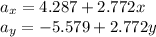
And so we find:

`a_x=4.287+2.772(-1)=1.515\\a_y=-5.579+2.772(5)=8.281`

And finally, we find the magnitude of the acceleration simply by applying Pythagorean's theorem:

`a=√(a_x^2+a_y^2)=√(1.515^2+8.281^2)=8.418`