Answer:
55km/h , 47.87° south west or 227.87°
Step-by-step explanation:
If there is no wind then the plane would be at a distance
d=(210 km/h)(0.49h) = 102.9 km west of the starting point.
if the wind is blown then then the plane is 121 km - 102.9 km = 18.1 km west and 20 km south in the time 0.49 h.
Velocity of the plane in west direction=(18.1 km) / 0.49 h = 36.9 km/h
velocity of the plane in south direction=(20 km) / 0.49 h = 40.8 km/h
Now the wind velocity is
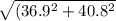
= 55.01 km/h
The direction is
θ =tan⁻¹ (40.8 / 36.9)
θ = 47.87° south west or 227.87°