Question

The rate constant of a reaction is 6.85 × 10−5 L/mol·s at 195°C and 2.20 × 10−3 L/mol·s at 258°C. What is the activation energy of the reaction? Enter your answer in scientific notation.

Answer 1

Answer: The activation energy of the reaction is 113.8 kJ/mol

Step-by-step explanation:

To calculate activation energy of the reaction, we use Arrhenius equation, which is:

`\ln((K_(258^oC))/(K_(195^oC)))=(E_a)/(R)[(1)/(T_1)-(1)/(T_2)]`

where,

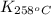`K_(258^oC)` = equilibrium constant at 258°C =
`2.20* 10^(-3)L/mol.s`

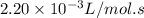
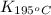`K_(195^oC)` = equilibrium constant at 195°C =
`6.85* 10^(-5)L/mol.s`

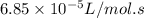
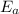`E_a` = Activation energy of the reaction = ?

R = Gas constant = 8.314 J/mol K

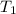`T_1` = initial temperature =
`195^oC=[195+273]K=468K`

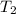`T_2` = final temperature =
`258^oC=[258+273]K=531K`

Putting values in above equation, we get:

`\ln((2.20* 10^(-3))/(6.85* 10^(-5)))=(E_a)/(8.314J/mol.K)[(1)/(468)-(1)/(531)]\\\\E_a=113780J/mol=113.8kJ/mol`

Hence, the activation energy of the reaction is 113.8 kJ/mol