Question

A reaction has a rate constant of 2.08 × 10−4 s−1 at 26 oC and 0.394 s−1 at 79 oC . Determine the activation barrier for the reaction. Enter your answer numerically and in terms of kJ/mol

Answer 1

Answer: The activation energy of the reaction is 124.6 kJ/mol

Step-by-step explanation:

To calculate activation energy of the reaction, we use Arrhenius equation, which is:

`\ln((K_(79^oC))/(K_(26^oC)))=(E_a)/(R)[(1)/(T_1)-(1)/(T_2)]`

where,

`K_(79^oC)` = equilibrium constant at 79°C =
`0.394s^(-1)`

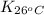`K_(26^oC)` = equilibrium constant at 26°C =
`2.08* 10^(-4)s^(-1)`

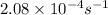
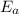`E_a` = Activation energy of the reaction = ?

R = Gas constant = 8.314 J/mol K

`T_1` = initial temperature =
`26^oC=[26+273]K=299K`

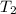`T_2` = final temperature =
`79^oC=[79+273]K=352K`

Putting values in above equation, we get:

`\ln((0.394)/(2.08* 10^(-4)))=(E_a)/(8.314J/mol.K)[(1)/(299)-(1)/(352)]\\\\E_a=124595J/mol=124.6kJ/mol`

Hence, the activation energy of the reaction is 124.6 kJ/mol