Question

Use the following scenario for all questions. The marketing manager of a grocery store observed customers going to the baby’s section. She found that 62% of all customers buy buby formula, 52% of all the customers buy diapers and 38% of all customers buy both baby formula and diapers. Use B to denote the event that a randomly selected customer buys baby formula and D to denote the event that a randomly selected customer buys diaper. Thus the information given above can be written as P(B)=0.62, P(D)=0.52 and P(B∩D)=0.38. _____________________________________________________________________________ What is the probability that a randomly selected customer buys either baby formula or diaper?

Answer 1

76% probability that a randomly selected customer buys either baby formula or diaper

Explanation

We solve this problem building the Venn's diagram of these probabilities.

There are two events, events B and D.

We have that:

`P(B) = P(b) + P(B \cap D)`

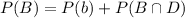
In which P(b) is the probability of only b and
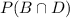`P(B \cap D)` is the probability of both B and D.

By the same logic, we have that:

`P(D) = P(d) + P(B \cap D)`

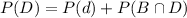
P(B)=0.62, P(D)=0.52 and P(B∩D)=0.38.

So

`P(D) = P(d) + P(B \cap D)`

`0.52 = P(d) + 0.38`

`P(d) = 0.14`

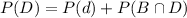
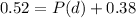
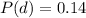
And

`P(B) = P(b) + P(B \cap D)`

`0.62 = P(b) + 0.38`

`P(b) = 0.24`

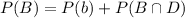
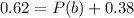
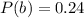
What is the probability that a randomly selected customer buys either baby formula or diaper?

`P(B \cup D) = P(b) + P(d) + P(B \cap D) = 0.24 + 0.14 + 0.38 = 0.76`

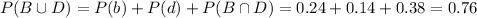
76% probability that a randomly selected customer buys either baby formula or diaper