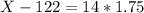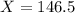Question

The systolic blood pressure (given in millimeters) of males has an approximately normal distribution with mean μ = 122 and standard deviation σ = 14. Kyle's doctor told him that the z-score for his systolic blood pressure is 1.75. (a)Which of the following is the best interpretation of this standardized score? Kyle's systolic blood pressure is 1.75 above the average systolic blood pressure of men his age. Kyle's systolic blood pressure is 1.75 times the average blood pressure of men his age. Kyle's systolic blood pressure is 1.75 standard deviations above the average systolic blood pressure for men. Kyle's systolic blood pressure is 175. (b) Calculate Kyle's blood pressure. (Enter an exact number as an integer, fraction, or decimal.)

Answer 1

a) Kyle's systolic blood pressure is 1.75 standard deviations above the average systolic blood pressure for men.

b) 146.5

Explanation:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this problem, we have that:

`\mu = 122, \sigma = 14`

Kyle's doctor told him that the z-score for his systolic blood pressure is 1.75.

So his systolic blood pressure is 1.75 standard deviations above the mean.

(a)Which of the following is the best interpretation of this standardized score?

Kyle's systolic blood pressure is 1.75 standard deviations above the average systolic blood pressure for men.

(b) Calculate Kyle's blood pressure. (Enter an exact number as an integer, fraction, or decimal.)

This is X when Z = 1.75.

`Z = (X - \mu)/(\sigma)`

`1.75 = (X - 122)/(14)`

`X - 122 = 14*1.75`

`X = 146.5`