Question

A 60,000 square meter rectangular yard is to be enclosed on three sides by wood fencing that costs $25.00 per meter and on the fourth side with a stone wall that will cost $40.00 per meter. What is the minimum cost of enclosing this yard as described?

Answer 1

`C'(y) = 50 -(3900000)/(y^2)=0`

And we can solve for y and we got:

`y = \sqrt{(3900000)/(50)}= 279.285`

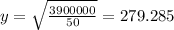
And using condition (1) we can solve for x and we got:

`x= (60000)/(279.285)= 214.834`

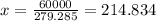
So then the minimum cost for this case would be:

`C = 50*279.285 + 65*214.834 = 27928.49`

Step-by-step explanation:

For this case the graph attached illustrate the problem for this case

We know that the total area is 60000, so then we have:

`xy = 60000`

If we solve for x we got:

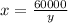`x = (60000)/(y)` (1)

Now we can define the cost function like this:

`C = 2*(25)*y + 25 x +40 x`

`C(x,y) = 50 y + 65 x`

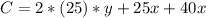
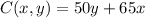
We can use the condition (1) and if we replace in the cost function we have:

`C(y) = 50 y + 65((60000)/(y))`

Since we need to minimize the cost, we can derivate the function in terms of y and we got:

`C'(y) = 50 -(3900000)/(y^2)=0`

And we can solve for y and we got:

`y = \sqrt{(3900000)/(50)}= 279.285`

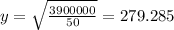
And using condition (1) we can solve for x and we got:

`x= (60000)/(279.285)= 214.834`

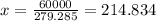
So then the minimum cost for this case would be:

`C = 50*279.285 + 65*214.834 = 27928.49`