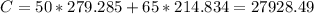Answer:
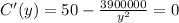
And we can solve for y and we got:
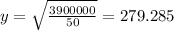
And using condition (1) we can solve for x and we got:
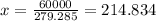
So then the minimum cost for this case would be:
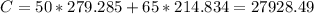
Step-by-step explanation:
For this case the graph attached illustrate the problem for this case
We know that the total area is 60000, so then we have:
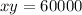
If we solve for x we got:
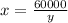 (1)
(1)
Now we can define the cost function like this:
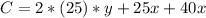
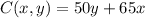
We can use the condition (1) and if we replace in the cost function we have:
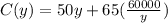
Since we need to minimize the cost, we can derivate the function in terms of y and we got:
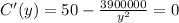
And we can solve for y and we got:
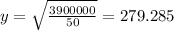
And using condition (1) we can solve for x and we got:
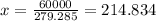
So then the minimum cost for this case would be: