Question

Determine the equations of the vertical and horizontal asymptotes, if any, for f(x) =2x/x+4

A. X=4,x = -2
--2. --4
C. X=-4, y = 2
d x--4, 7--2
Please select the best answer from the choices provided

Answer 1

Option C:
`x=-4` ,
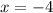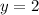`y=2` is the asymptotes of the equation.

Step-by-step explanation:

The equation is
`f(x)=(2x)/(x+4)`

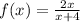
The vertical asymptote of the equation can be determined by equating the denominator of the equation to zero.

Thus, we have,

`x+4=0`

`x=-4`

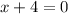
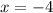
Hence, the vertical asymptote of the function is
`x=-4`

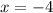
Now, we shall determine the horizontal asymptote.

The horizontal asymptote of the function can be determined by dividing the leading coefficient of x in the numerator by the leading coefficient of x in the denominator.

Thus, we have,

`y=(2)/(1)`

`y=2`

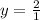
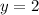
Hence, the horizontal asymptote of the function is
`y=2`

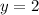
Therefore, Option C is the correct answer.