Question

Carbonyl fluoride, COF2, is an important intermediate used in the production of fluorine-containing compounds. For instance, it is used to make the refrigerant carbon tetrafluoride, CF4 via the reaction 2COF2(g)⇌CO2(g)+CF4(g), Kc=6.30 If only COF2 is present initially at a concentration of 2.00 M, what concentration of COF2 remains at equilibrium?

Answer 1

Answer: The equilibrium concentration of
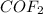`COF_2` is 0.332 M

Step-by-step explanation:

We are given:

Initial concentration of
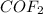`COF_2` = 2.00 M

The given chemical equation follows:

`2COF_2(g)\rightleftharpoons CO_2(g)+CF_4(g)`

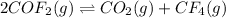
Initial: 2.00

At eqllm: 2.00-2x x x

The expression of
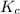`K_c` for above equation follows:

`K_c=([CO_2][CF_4])/([COF_2]^2)`

We are given:

`K_c=6.30`

Putting values in above expression, we get:

`6.30=(x* x)/((2.00-2x)^2)\\\\x=0.834,1.25`

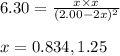
Neglecting the value of x = 1.25 because equilibrium concentration of the reactant will becomes negative, which is not possible

So, equilibrium concentration of
`COF_2=(2.00-2x)=[2.00-(2* 0.834)]=0.332M`

Hence, the equilibrium concentration of
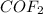`COF_2` is 0.332 M