Question

Compute the boiling point elevation of a salt water solution that contains 3.80 g of NaCl dissolved in 122 mL of water. Enter the number of degrees celsius that the boiling point will be elevated.

Answer 1

Answer: The boiling point elevation of salt water solution is 0.55°C

Step-by-step explanation:

To calculate the mass of water, we use the equation:

`\text{Density of substance}=\frac{\text{Mass of substance}}{\text{Volume of substance}}`

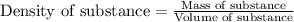
Density of water = 1 g/mL

Volume of water = 122 mL

Putting values in above equation, we get:

`1g/mL=\frac{\text{Mass of water}}{122mL}\\\\\text{Mass of water}=(1g/mL* 122mL)=122g`

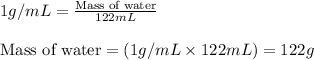
To calculate the elevation in boiling point, we use the equation:

`\Delta T_b=iK_bm`

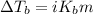
Or,

`\Delta T_b=i* K_b* \frac{m_(solute)* 1000}{M_(solute)* W_(solvent)\text{ (in grams)}}`

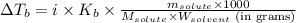
where,

`\Delta T_b` = ?

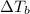i = Vant hoff factor = 2 (For NaCl)

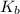`K_b` = molal boiling point elevation constant = 0.52°C/m.g

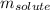`m_(solute)` = Given mass of solute (NaCl) = 3.80 g

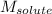`M_(solute)` = Molar mass of solute (NaCl) = 58.55 g/mol

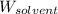`W_(solvent)` = Mass of solvent (water) = 122 g

Putting values in above equation, we get:

`\Delta T_b=2* 0.52^oC/m* (3.80* 1000)/(58.55g/mol* 122)\\\\\Delta T_b=0.55^oC`

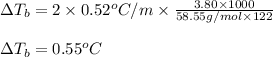
Hence, the boiling point elevation of salt water solution is 0.55°C