Question

A radioactive substance decays exponentially. A scientist begins with 200 milligrams of a radioactive substance. After 17 hours, 100 mg of the substance remains.How many milligrams will remain after 24 hours?

Answer 1

75.17 mg of the radioactive substance will remain after 24 hours.

Answer:

Step-by-step explanation:

Any radioactive substance will obey the exponential decay behavior. So according to this behavior, any radioactive substance will be decaying in terms of exponential form of disintegration constant and Time.

Disintegration constant is the rate of decay of radioactive elements. It can be measured using the half life time of the radioactive element .While half life time is the time taken by any radioactive element to decay half of its concentration. Like in this case, at first the scientist took 200 mg then after 17 hours, it got reduced to 100 g. So the half life time of this element is 17 hours.

Then Disintegration constant = 0.6932/Half Life time

Disintegration constant = 0.6932/17=0.041

Then as per the law of disintegration constant:

`N = N_(0)e^(-xt)`

Here N is the amount of radioactive element remaining at time t and
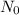`N_(0)` is the initial amount of sample, x is the disintegration constant.

So here,
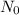`N_(0)` = 200 mg, x = 0.041 and t = 24 hrs.

N = 200 ×
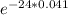`e^(-24*0.041)` =75.17 mg.

So 75.17 mg of the radioactive substance will remain after 24 hours.