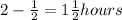Question

Beatrice participates in professional triathlons. She runs 2 mph faster than her friend Joe, a weekend athlete. If they each

run 12 mi, Beatrice finishes 30 min ahead of Joe. Determine how fast each person runs.

Answer 1

Speed of Joe is 6 mph and that of Beatrice is 8 mph

Explanation:

Let Joe's speed be S

Beatrice's speed be s + 2

Let Joe's time be T

Beatrice's time = T - 1/2

Then

We know that

`speed = (distance)/(time)`

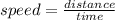
Now

Distance =
`speed * time`

On substituting the value

Equation corresponding to Joe

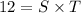`12 = S * T`...........................(1)

Equation corresponding to Beatrice

`(S+2) * (T - (1)/(2))=12`

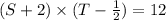
Now solving for s and T,we get

`(S+2) * ((12)/(S)- (1)/(2))=12`

`(S+2) * ((24 -S)/(2S))=12`

`2S(S+2) * ({24 -S})=12(2S)`

`(2S^2 - 4S )(24-S) = 24S`

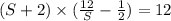
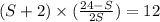
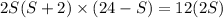
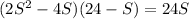
S = 6 mph -------------------------- Joe's speed

T = 2 hours ------------------------ Joe's time

Thus Beatrice's speed is

6 + 2 = 8 mph

Beatrice's time is

`2 -(1)/(2) =1(1)/(2 )hours`