Plz solve this question Its urgent.....

Question

asked Oct 19, 2021 186k views

1 Answer

Rotskoff · Answer 1 · 2021-10-26T09:50:24+0000

Answer:

Explanation:

tan Θ + tan 2Θ + √3 tan Θ tan 2Θ = √3

tan Θ + tan 2Θ = √3 - √3 tan Θ tan 2Θ

tan Θ + tan 2Θ = √3 ( 1 - tan Θ tan 2Θ)

(tan Θ + tan 2Θ) / (1 - tanΘ tan 2Θ) = √3

tan(Θ + 2Θ) = √3

tan 3Θ = tan (
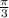$(\pi )/(3)$ ) we know tan Θ = tan α; Θ = nΠ + α, n belongs to z

3Θ = nΠ + Π/3

Θ = nπ/3 + Π/9 for all n in Z