Question

A wire of resistivity ? must be replaced in a circuit by a wire four times as long. If, however, the

total resistance is to remain as before, the diameter of the new wire must
A) be two times smaller.
B) be four times larger.
C) remain unchanged.
D) be four times smaller.
E) be two times larger.

Answer 1

E) be two times larger.

Step-by-step explanation:

As we know that the relation between the resistance and the resistivity of the wire is given as:

`R=\rho.(l)/(a)`

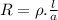
where:

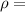`\rho=` resistivity of the wire

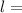`l=` length of wire

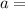`a=` area of wire

`R=` resistance

Now, when the length of the wire is four times the initial length then for the resistance to remain constant:

`R=\rho.(4l)/(a')`

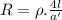
where:

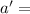`a'=` area of the new wire

`\rho.(l)/(a) =\rho.(4l)/(a')`

`a'=4a`

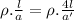
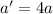
we know that area of the cross section of wire is given as:

`a=\pi.r^2`

`\pi.r'^2=4* \pi.r^2`

`r'=2r`

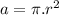
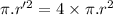
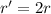
Hence the radius must be twice of the initial radius for the resistance to be constant when length is taken four times.