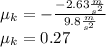Question

A 6 kg box with initial speed 5 m/s slides across the floor and comes to a stop after 1.9 s. What is the coefficient of kinetic friction?

Answer 1

`\mu_k=0.27`

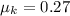
Step-by-step explanation:

According to the free body diagram, in this case, we have:

`\sum F_x:-F_k=ma\\\sum F_y:N=mg`

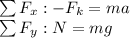
Recall that the force of friction is given by:

`F_k=\mu_k N`

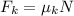
Replacing and solving for the coefficient of kinetic friction:

`-\mu_kN=ma\\-\mu_k(mg)=ma\\\mu_k=-(a)/(g)`

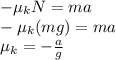
We have an uniformly accelerated motion. Thus, the acceleration is defined as:

`a=(v_f-v_0)/(t)\\a=(0-5(m)/(s))/(1.9s)\\a=-2.63(m)/(s^2)`

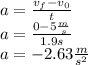
Finally, we calculate
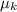`\mu_k`:

`\mu_k=-(-2.63(m)/(s^2))/(9.8(m)/(s^2))\\\mu_k=0.27`