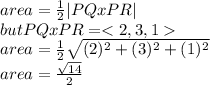Question

Consider the points below. P(1, 3, 5), Q(−4, 7, 3), R(2, 2, 6)

(a) Find a nonzero vector orthogonal to the plane through the points P, Q, and R.
(b) Find the area of the triangle PQR.

Answer 1

a. <2,3,1>

b.
`(√(14) )/(2)`

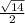
Explanation:

From the data given, we have point

P(1,3,5)

Q(-4,7,3)

R(2,2,6)

a. For us to find a vector orthogonal to the plane through the points P,Q and R we define two vectors such as

PQ=<-4,7,3>-<1,3,5>

PQ=<-5,4,-2>

we also define PR

PR=<2,2,6>-<1,3,5>

PR=<1,-1,1>

The cross product of the two formed vector gives rise to a vector that is orthogonal to the given plane Hence we carry out the cross product

`\left[\begin{array}{ccc}i&j&k\\-5&4&-2\\1&-1&1\end{array}\right] \\i(4-2)-j(-5+2)+k(5-4)\\2i+3j+k\\`

Hence the required vector is <2,3,1>

b. The area of the formed triangle can be expressed as

`area=(1)/(2)|PQxPR|\\but PQxPR=<2,3,1>\\ area=(1)/(2)\sqrt{(2)^(2)+(3)^(2)+(1)^(2)}\\ area=(√(14))/(2)`