Answer:
211.2 N
Step-by-step explanation:
Data provided in the question:
Mass of child, m = 33.0 kg
Distance from the center, r = 2.50 m
Tangential speed, v = 4.00 m/s
Now,
Magnitude of the centripetal force,
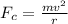
Thus, on putting the values, we get
Magnitude of the centripetal force,

or
Magnitude of the centripetal force,
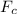 = 211.2 N
= 211.2 N