Question

A cylindrical roller with diameter 77 cm and height 1 m is used to level a rectangular park with dimensions22 × 11 . Find the number of revolutions required to level the park.

Answer 1

Answer: The number of revolutions required to level the park is 100.

Explanation:

Given : Diameter of roller = 77 cm

Then radius of roller : r =
`(77)/(2)\ cm`

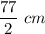
Height = 1 m = 100 cm

Curved surface area of roller =
`2\pi rh= 2*(22)/(7)*(77)/(2)*100=24200\ cm^2`

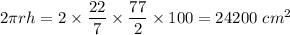
Dimensions of park = 22 × 11 m

Then Area of park =
`22*11\ m^2= 232\ m^2=232*100*100 \ cm^2`

`=2420000\ cm^2`

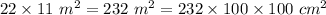
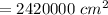
Now , the number of revolutions required to level the park = (Area of park) ÷ (Curved surface area of roller )

`2420000/ 24200=100`

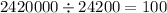
Hence, the number of revolutions required to level the park is 100.