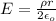Question

An infinite cylindrical rod has a uniform volume charge density rho (where rho>0). The cross section of the rod has radius r0. Find the magnitude of the electric field E at a distance r from the axis of the rod. Assume that r

Considering the symmetry of the charge distribution, choose one of the following options as the most appropriate choice of Gaussian surface to use in this problem.

A) a finite closed cylinder whose axis coincides with the axis of the rod and whose cross section has radius r0
B) a finite closed cylinder whose axis coincides with the axis of the rod and whose cross section has radius r1 C) a sphere of radius r D) a finite closed cylinder whose axis coincides with the axis of the rod and whose cross section has radius r E) an infinite cylinder whose axis coincides with the axis of the rod and whose cross section has radius r

Answer 1

`E=(\rho r)/(2 \epsilon_o)`

option D

Step-by-step explanation:

The correct choice of Gaussian surface would be (D) a finite closed cylinder whose axis coincides with the axis of the rod and whose cross-section has a radius of
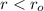`r<r_o`. This is because the charged cylinder is of infinite length and hence there won't be any electric flux coming out of the top and bottom flat surfaces.

Now, to find out the magnitude of the electric field
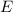`E`, we shall have to apply Gauss's law,

`\int {E} \, dA=(Q_(enclosed))/(\epsilon_o)`

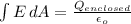
or,
`E.2\pi r h=(\rho* \pi r^2h)/(\epsilon_o)` (
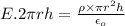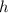`h` being the height of the Gaussian cylinder)

or,
`E=(\rho r)/(2 \epsilon_o)`