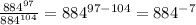Answer:
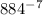
Explanation:
Start by simplifying the denominator of the fraction. When multiplying exponents of the same base, you can add the exponents. This is also known as the product rule.
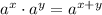
["a" is the base, and "x" and "y" are the exponents]
Using this we find...
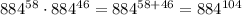
When dividing exponents of the same base, you can subtract the exponents. This is also knows as the quotient rule.
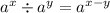
Using this we find...