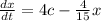Question

A fish tank initially contains 15 liters of pure water. Brine of constant, but unknown, concentration of salt is flowing in at 4 liters per minute. The solution is mixed well and drained at 4 liters per minute. Let x be the amount of salt, in grams, in the fish tank after t minutes have elapsed.

a. Find a formula for the rate of change in the amount of salt, dx/dt, in terms of the amount of salt in the solution x and the unknown concentration of incoming brine c.
dx/dt = _______

Answer 1

`(dx)/(dt)=4c-(4)/(15)x`

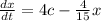
Explanation:

Data provided in the question:

Initial volume of water = 15 liters

Concentration of salt = 4 liters per minute

x be the amount of salt, in grams, in the fish tank after t minutes have elapsed

The unknown concentration of incoming brine c.

Now,

Salt concentration per minute =
`(4)/(15)`

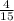
For x amount of salt =
`(4)/(15)x`

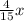
Therefore,

`(dx)/(dt)=4c-(4)/(15)x`