Answer:
The answer to the question is;
The change in entropy ΔS of the system ≈ 1.43 × 10⁻²³ J·K⁻¹.
Step-by-step explanation:
The Boltzmann Entropy Equation is
S = K×㏑W
Where W = number of different micro-states
Since the total initial Kinetic energy of the system is 22ε where the number of possible states are ε, 2ε, 3ε,...., 22ε we have 22 micro-states
Similarly since the final rotational kinetic energy rises is 62ε we have 62 states
The Change in entropy then is
ΔS = Final entropy - Initial Entropy
ΔS = K×㏑W
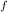- K×㏑W
Where
W
= Total initial micro-states = 22
W
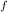= Final total micro-states = 62
K = Boltzmann constant = 1.38064852 × 10⁻²³ m²·kg·s⁻²·K⁻¹
we have ΔS = K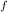×(㏑W
- ㏑W
)
= 1.38064852 × 10⁻²³ m²·kg·s⁻²·K⁻¹×(㏑(62) - ㏑(22))
= 1.38064852 × 10⁻²³ m²·kg·s⁻²·K⁻¹×(4.13 - 3.091)
ΔS = 1.430480636 × 10⁻²³ m²·kg·s⁻²·K⁻¹.
Where 1 m²·kg·s⁻² = 1 J
ΔS ≈ 1.43 × 10⁻²³ m²·kg·s⁻²·K⁻¹ = 1.43 × 10⁻²³ J·K⁻¹.