Question

A large lake is stocked with 10% catfish. You go out on the lake to fish, and each fish you catch that is not a catfish is thrown back into the lake. (Assume that each time you catch a fish, it is independent of the other fish you have caught.) Let X be the number of tries it takes until you catch your first catfish.

(a) What is the average (expected) value for X?
(b) What is the probability that X is at most 3?

Answer 1

a.) Expected value = 10.

b.) The probability that X is at most 3 = 0.271

Explanation:

A large lake is stocked with 10% catfish.

Every fish caught that is not a catfish is thrown back.

X is the number of tries before we catch our first catfish.

We can say that the distribution is X
`\sim` Geo( p = 0.1).

In a geometric distribution we can have only two outcomes of a particular trial and that is it will either be a success or a failure.

a.) The average or expected value is
`E(X) = (1)/(p) = (1)/(0.1) = 10`.

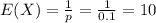b.) X is at most three

p(X ≤ 3) = p(X = 1) + p(X = 2) + p(X = 3)

= 0.1 + ( 0.1 × 0.9) + ( 0.1 ×
`(0.9)^2`)

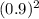= 0.1 + 0.09 + 0.081

= 0.271