Question

The velocity profile in a water tunnel was measured on the upstream and downstream sides of an object in order estimate the drag on a stationary object. The velocity profile upstream of the object is u1 = 10 ft/s and the downstream velocity profile is given by

Answer 1

R_x = 49.78 lb/ft

Step-by-step explanation:

Given:

- The velocity u_1 upstream = 10 ft/s

- Pressure field p_1 = p_2 = 10 psig

- The velocity profile downstream is given by:

u_2 = 10 ft/s ...... |y| >= 2

u_2 = 10 - 3/8*(2 - |y| )^2 ....... |y| < 2

- The profiles are given in attachment.

Find:

Determine the drag force per unit length.

Solution:

- Develop a control volume around the object see attachment which only consists of water. Then apply principle of linear momentum along the x-direction. It can be expressed as:

`-p_w*u_1^2*A_1 + 2 \int\limits^2_0 {u_2^2*p_w} \, dy = -F_x\\p_w*u_1^2*h - 2*p_w \int\limits^2_0 {u_2^2} \, dy = R_x`

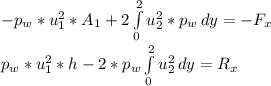
Where, p_w: Density of water = 1.94 slugs/ft^3

h : Vertical height of control volume

R_x: The reaction force exerted by object on control volume(Drag)

- To determine h, The conservation of mass principle is applied at sections 1 and 2:

`p_w*u_1*h = 2\int\limits^2_0 ({p_w*u_2}) \, dy \\h = (2)/(u_1) \int\limits^2_0 ({10-(3*(2-y)^2)/(8) } )\, dy \\\\h = (2)/(u_1) \limits^2_0 ({10y+((2-y)^3)/(8) } )\,\\\\h = (2)/(10)*({20 + 0 - 0-1 ) = 3.8 ft`

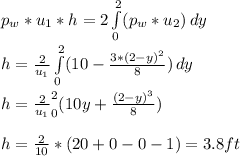
- Now for Drag force per unit length we have:

`p_w*u_1^2*h - 2*p_w \int\limits^2_0 {(10-(3*(2-y)^2)/(8) )^2} \, dy = R_x\\\\p_w*u_1^2*h - 2*p_w \int\limits^2_0 ({100+(9*(2-y)^4)/(64)-(15*(2-y)^2)/(2)}) \, dy = R_x\\\\p_w*u_1^2*h - 2*p_w * ({100y-(9*(2-y)^5)/(320)+(5*(2-y)^3)/(2)}) \limits^2_0 = R_x\\\\1.94*10^2*3.8 - 2*1.9*({200+(9)/(10)-20}) = R_x\\\\R_x = 737.2 - 687.42\\\\R_x = 49.78 lb/ft`

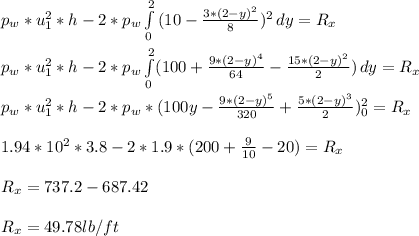
- The drag force per unit length on the object is given by R_x = 49.78 lb/ft. It is also the reaction developed due to change in momentum of fluid.