Question

A cellular telephone tower that is 100 feet tall is placed on top of a mountain that is 1300 feet above sea level. What is the angle of depression from the top of the tower to a cell phone user who is 7 horizontal miles away and 300 feet above sea level?

Answer 1

Angle of depression from top of the tower is 88.29°

Step-by-step explanation:

The height of tower = 100 feet.

The height of mountain above sea level = 1300 feet.

So the total vertical height of tower = 100 feet + 1300 feet = 1400 feet.

The horizontal distance of cell phone user from tower = 7 miles = (7 * 5280) feet = 36960 feet.

The vertical distance of cell phone user from sea level = 300 feet.

The vertical height of cell phone user from the top of the tower = (1400 - 300) feet = 1100 feet.

Let the angle of depression from top of tower be ' ∅ ' .

Here we can see that a right angle triangle is formed with base = 1100 feet and perpendicular side = 36960 feet.

We know that ,

tan∅ =
`(perpendicular)/(base) = (36960)/(1100)` = 33.6

∅ =
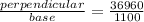`\tan^(-1)`33.6

∅ = 88.29°

So the angle of depression from the top of the tower is 88.29°.