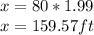Answer:
159.57 Feet Horizontally from the foot of the wall
Step-by-step explanation:
Given Data:
Height =
 = 64 feet
= 64 feet
gravitational acceleration = g = 32.17
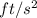
Initial Vertical Velocity component

Initial Horizontal Velocity Component
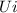 = 80
= 80

To find = Time taken to reach ground =
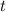
Horizontal Distance from the foot of the wall =
 = ?
= ?
Calculation:
From the equation of motion
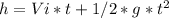 ........ (1) (in terms of Vertical component of velocity).
........ (1) (in terms of Vertical component of velocity).
Putting in values in the above equation.
 (Time taken to reach the ground)
(Time taken to reach the ground)
Now, to find

we use the same equation of motion we used above but this time we solve for the horizontal component of Velocity
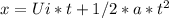

Putting in values in the above equation.