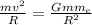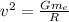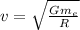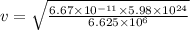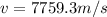Question

A satellite m = 500 kg orbits the earth at a distance d = 245 km, above the surface of the planet. The radius of the earth is re = 6.38 × 106 m and the gravitational constant G = 6.67 × 10-11 N m2/kg2 and the Earth's mass is me = 5.98 × 1024 kg. What is the speed of the satellite in m/s?

Answer 1

`7759.3m/s`

Step-by-step explanation:

We are given that

Mass of satellite=
`m=500 kg`

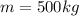
Distance, d=245 km=
`245000m`

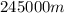
Using 1km=1000m

Radius of the earth=
`r_e=6.38* 10^6`m

`G=6.67* 10^(-11)Nm^2/kg^2`

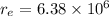Mass of earth,
`m_e=5.98* 10^(24) Kg`

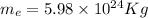
We have to find the speed of the satellite.

Radius of orbit=
`R=r_e+d=245000+6.38* 10^6=6.625* 10^6m`

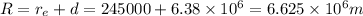
Centripetal force of satellite=Gravitational force

`(mv^2)/(R)=(Gmm_e)/(R^2)`

`v^2=(Gm_e)/(R)`

`v=\sqrt{(Gm_e)/(R)}`

`v=\sqrt{(6.67* 10^(-11)* 5.98* 10^(24))/(6.625* 10^6)}`

`v=7759.3m/s`