Answer:
The four values of f are given in part a of the question as
f= 0.30, 0.50, 0.70, 0.90
The answers to the question are
i. icy road, f = 0.3
ii. Very good road with great tires, f = 0.9
iii. Asphalt road with fair tires, f = 0.7
iv. Wet road with fair tires, f = 0.5
Explanation:
The braking distance is given by
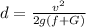 Where
Where
d = Braking distance
f = Coefficient of friction
G = Constant = Grade of the road and
g = Acceleration due to gravity = 32.19 ft/s²
Where v = 60 mph we have
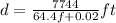
Therefore for
f = 0.3, d = 400.41 ft
f = 0.5, d = 240.35 ft
f = 0.7, d = 171.71 ft
f = 0.9, d = 133.56 ft
From the breaking distance required we have
i. icy road, f = 0.3
ii. Very good road with great tires, f = 0.9
iii. Asphalt road with fair tires, f = 0.7
iv. Wet road with fair tires, f = 0.5