Question

An investment will pay $100 at the end of each of the next 3 years, $250 at the end of Year 4, $400 at the end of Year 5, and $500 at the end of Year 6.A) If other investments of equal risk earn 6% annually, what is its present value? Round your answer to the nearest cent.B) If other investments of equal risk earn 6% annually, what is its future value? Round your answer to the nearest cent.

Answer 1

Present value = $1,117

Future value = $1,585

Step-by-step explanation:

Given:

1st investment (C1) = $100

Number of year = 3

2nd Investment(C2) = $200 ( 4th year)

3rd Investment(C3) = $300 (5th year)

4th Investment(C4) = $500 (6th year)

rate of interest = 6% = 0.06

Present value :

`Present \ value = (C1)/((1+R)^1) +(C1)/((1+R)^2)+ (C1)/((1+R)^3) +(C2)/((1+R)^4) +(C3)/((1+R)^5)+ (C4)/((1+R)^6) \\Present \ value = (100)/((1+0.06)^1) +(100)/((1+0.06)^2)+ (100)/((1+0.06)^3) +(250)/((1+0.06)^4) +(400)/((1+0.06)^5)+ (500)/((1+0.06)^6)`

`Present \ value = (100)/((1.06)^1) +(100)/((1.06)^2)+ (100)/((1.06)^3) +(250)/((1.06)^4) +(400)/((1.06)^5)+ (500)/((1.06)^6) \\Present \ value = (100)/((1.06)) +(100)/((1.1236))+ (100)/((1.191)) +(250)/((1.2624)) +(400)/((1.3382))+ (500)/((1.4185)) \\Present \ value =94.39+88.99+83.96+198.03+298.90+352.48\\ =1116.75`

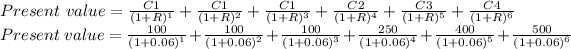
Present value = $1,116.75 = $1,117

Future Value:

`Future Value =PV (1+r)^n\\= 1,117(1+0.06)^6\\= 1,117(1.06)^6\\=1,117(1.4185)\\=1,584.50`

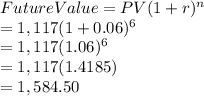
Future value = $1,585