Answer:
Pressure drop across the contraction section = 133 kPa
The pressure difference due to frictional losses is = 39.7 kPa
The pressure difference due to kinetic energy changes = 93 kPa
Step-by-step explanation:
If
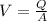 -----------equation (1)
-----------equation (1)
where ;
V = velocity
Q = flow rate
A = area of cross-section
As we know that Area (A) =
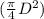
substituting
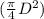 for A in equation (1); we have:
for A in equation (1); we have:
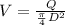
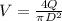 ----------------- equation (2)
----------------- equation (2)
Now, having gotten that; lets find out the corresponding velocity
 of the water at point (1) of the pipe and velocity
of the water at point (1) of the pipe and velocity
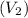 of the water at point 2 using the derived formula.
of the water at point 2 using the derived formula.
For velocity
 :
:
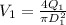
From, the question; we are given that:
water flow rate at point 1
 =
=
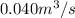
Diameter of the pipe at point 1
 = 0.12 m
= 0.12 m
∴
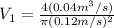
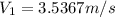
For velocity
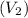 :
:
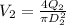
water flow rate at point
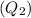 =
=
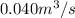
Diameter of the pipe at point 2
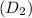 = 0.06 m
= 0.06 m
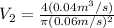
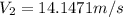
Similarly, since we have found out our veocity; lets find the proportion of the area used in both points. So proportion of
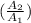 can be find by replacing
can be find by replacing
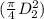 for
for
 and
and
 for
for
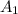 .
.
So:
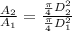
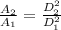

= 0.25
However, let's proceed to the phase where we determine the pressure drop across the contraction Δp by using the expression.
Δp =
![[(p_(water))/(2) (V_2^2-V_1^2)+ (p_(water))/(2) K_LV_2^2]](https://img.qammunity.org/2021/formulas/chemistry/high-school/ql60ovwe8ya3gu10lh1a6m1bo2jsrqo81k.png)
where;
 = standard frictional loss coefficient for a sudden contraction which is 0.4
= standard frictional loss coefficient for a sudden contraction which is 0.4
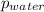 = density of the water = 999 kg/m³
= density of the water = 999 kg/m³
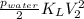 = pressure difference due to frictional losses.
= pressure difference due to frictional losses.
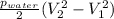 = pressure difference due to the kinetic energy
= pressure difference due to the kinetic energy
So; we are calculating three terms here.
a) the pressure drop across the contraction = Δp
b) pressure difference due to frictional losses. =
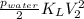
c) pressure difference due to the kinetic energy =
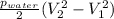
a) Δp =
![[(p_(water))/(2) (V_2^2-V_1^2)+ (p_(water))/(2) K_LV_2^2]](https://img.qammunity.org/2021/formulas/chemistry/high-school/ql60ovwe8ya3gu10lh1a6m1bo2jsrqo81k.png)
Δp =
![[(999kg/m^3)/(2) ((14.1m/s)^2-(3.53m/s)^2)+ (999kg/m^3)/(2) (0.4)(14.1m/s)^2]](https://img.qammunity.org/2021/formulas/chemistry/high-school/1batwyucctikd7s53cmpten7ztgoj6u7jr.png)
Δp = [(93081.375) + (39722.238)]
Δp = (93 kPa) + (39.7 kPa)
Δp = 132.7 kPa
Δp ≅ 133 kPa
∴ the pressure drop across the contraction Δp = 133 kPa
the pressure difference due to frictional losses
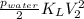 = 39.7 kPa
= 39.7 kPa
the pressure difference due to the kinetic energy
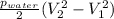 = 93 kpa
= 93 kpa
I hope that helps a lot!