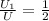Question

An air-gap, parallel plate capacitor with area A and gap width d is connected to a battery that maintains the plates at potential difference V. (a) The plates are pulled apart, doubling the gap width, while they remain in electrical contact with the battery terminals. By what factor does the potential energy of the capacitor change?

Answer 1

The new potential energy decreases by the factor of 2 to the old potential energy.

Step-by-step explanation:

Capacitance of a parallel plate capacitor is given by the relation :

C = (ε₀A)/d

Here ε₀ is vacuum permittivity, A is area of the capacitor plate and d is the distance between them.

Potential energy of the capacitor, U =
`(1)/(2)CV^(2)`

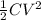
Here V is the potential difference between the plates.

According to the problem, the distance between the plates get double but area remains same. So,

d₁ = 2d

Here d₁ is new distance between the plates.

Hence, new capacitance is :

C₁ = (ε₀A)/d₁ = (ε₀A)/2d = C/2

The capacitor have same potential difference that is V. Hence, the new potential energy is :

U₁ =
`(1)/(2)C_(1) V^(2)` =
`(1)/(2)(C)/(2) V^(2)`

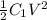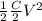
U₁ = U/2

`(U_(1) )/(U) = (1)/(2)`